Let x be the number of miles and y the total cost; therefore, the equations that model the two plans are
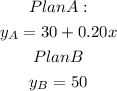
Then, set y_A=y_B as shown below
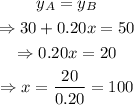
Therefore, once the mileage is greater than 100 miles, the total cost of plan B will be less than that of plan A.
The answer is 100 miles.