Question

Given the function h(x) = x^2 – 7x + 6, determine the average rate of change of the function over the interval 3 < x < 7.hurry please need answer.

Answer 1

Answer:Explanation:

The average rate of change = 3

The average rate of change for a function f(x) is an intervale a < x < b can be calculated using the following equation:

`\frac{f(b)-f(a)_{}}{b-a}`

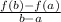
Therefore, the average rate of change of the function h(x) = x^2 – 7x + 6 in the interval 3 < x < 7 is:

`(h(7)-h(3))/(7-3)`

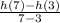
Where h(7) and h(3) are equal to:

`\begin{gathered} h(7)=7^2-7(7)+6 \\ h(7)=49-49+6 \\ h(7)=6 \\ h(3)=3^2-7(3)+6 \\ h(3)=9-21+6 \\ h(3)=-6 \end{gathered}`

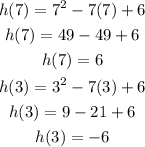
So, the average rate of change is:

`(6-(-6))/(7-3)=(6+6)/(4)=(12)/(4)=3`

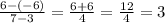
Therefore, the answer is 3.