Question

Hello can you help me with this trigonometry question please

Answer 1

Question:

On a circle of radius 6 feet, what angle would subtend an arc of lenght 5 feet?

nswer:

he frormula for the lenght of arc (s) given an angle theta (in radians) and a radius R is:

`S=\theta R`

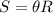
We'll just have to clear theta from this equation, and convert it to degrees.

`\begin{gathered} S=\theta R\rightarrow(S)/(R)=\theta \\ \theta=(5)/(6)\text{ radians} \\ To\text{ convert from radians to degrees, multiply by }(180)/(\pi) \\ \theta=(5)/(6)*(180)/(\pi)\rightarrow\theta=47.74\text{ degrees} \end{gathered}`

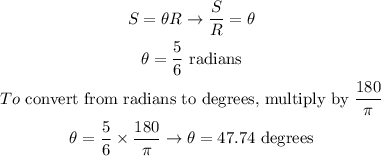
Therefore, the angle that would subtend an arc of lenght 5 feet on a circle of radius 6 feet is 47.74°