You have to determine which of the given square roots can be expressed as a fraction:
1) The square root of one is 1
![\sqrt[]{1}=1](https://img.qammunity.org/2023/formulas/mathematics/college/z6tj5f3g4ddgpu07b9e7frt5v5s24z4vzq.png)
One can be expressed as a fracion:
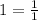
So it is a rational number.
2) The square root of 2 is an irrational number and cannot be expressed as a fraction.
![\sqrt[]{2}=1.414213562\ldots..](https://img.qammunity.org/2023/formulas/mathematics/college/l4ii74i90ujwcuml1ggfddu89e9efi3rop.png)
Its decimal expantion has no end, i.e. it has infinite decimal values.
3) Square root of three is an irrational number and cannot be expressed as a fraction.
![\sqrt[]{3}=1.732050808\ldots.](https://img.qammunity.org/2023/formulas/mathematics/college/iqikrr1a4uw9v5k72bm1meyejg1to34x1j.png)
4) The square root of 5 is an irrational number and cannot be expressed as a fraction.
![\sqrt[]{5}=2.236067977\ldots..](https://img.qammunity.org/2023/formulas/mathematics/college/6zzgw6zzwi3h0gic1l1d506yjlwxecbm89.png)
In conclusion the only rational number in the given set is the square root of 1.