Notice that s stands for the slant height of the pyramid, and this height is the height of each one of the lateral triangular faces.
We will need to use the next formulas
![\begin{gathered} A_{\text{hex}}=\frac{3\sqrt[]{3}}{2}a^2\to\text{Area of a regular hexagon (a is one of its sides)} \\ A_{\text{tri}}=(bh)/(2)\to\text{Area of a triangle} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7qqzyfunloyr5chx9m41s50847htyh46vc.png)
Therefore, the surface area is
![\begin{gathered} A_{\text{figure}}=A_{\text{hex}}+6\cdot A_{\text{tri}}=\frac{3\sqrt[]{3}(3)^2}{2}+6\cdot((3\cdot10.3))/(2) \\ =\frac{27\sqrt[]{3}}{2}+92.7 \\ \Rightarrow A_{\text{figure}}=\frac{27\sqrt[]{3}}{2}+92.7 \\ \Rightarrow A_{\text{figure}}\approx23.4+92.7=116.1 \\ \Rightarrow A_{\text{figure}}=116.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vh0cxip9l3zziwtsst3bzfi5ldegxxy1qu.png)
Lateral Area=116.1 m^2
As for the volume, the volume of a regular pyramid is
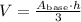
In our case,
![V=\frac{3\sqrt[]{3}a^2}{2}\cdot(h)/(3)=\frac{\sqrt[]{3}}{2}a^2h](https://img.qammunity.org/2023/formulas/mathematics/college/ln1iqs4ucibsklrnu9lo2ymcjfdfveveck.png)
Therefore,
![\Rightarrow V=\frac{\sqrt[]{3}}{2}(3)^2\cdot10=45\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/6p5n6q0it9d2h1rn8sobztl7sctizd11ht.png)
Volume= 77.9 m^3