30
Step-by-step explanation:
Angle = 67°
To solve the question, we will use an illustration:
To get the horizontal distance from the base of the skycrapper to the ship, we will apply tangent ratio:
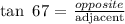
opposite = 903 ft
adjacent = horizontal distance from the base of the skycrapper to the ship = x
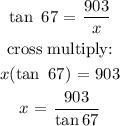
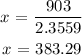
To the nerest hundredth, the horizontal distance from the base of the skycrapper to the ship is 383.30ft