Question

I need help with this problem

Answer 1

We have the following function:

`H(t)=10\sin (2\pi(t-(1)/(4)))+15`

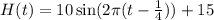
a) The initial height occurs at t=0. By substituting this value into the function, we get

`H(0)=10\sin (2\pi(0-(1)/(4)))+15`

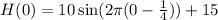
which gives

`\begin{gathered} H(0)=10\sin (-2\pi(1)/(4))+15 \\ H(0)=10\sin (-(2\pi)/(4))+15 \\ H(0)=10\sin (-(\pi)/(2))+15 \end{gathered}`

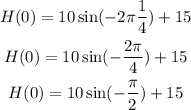
since sin(-Pi/2) is equal to -1, we have

`H(0)=-10+15`

Then, H(0)= 5, so the height is 5 feets.

b) The car will make a full rotation when the argument is shifted 2Pi:

`H(t)=10\sin (2\pi(t-(1)/(4))+2\pi)+15`

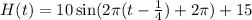
at this point H(t) must be equal to 5 feets. Then, we have

`5=10\sin (2\pi(t-(1)/(4))-2\pi)+15`

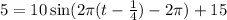
and we must find t. If we move +15 to the left hand side, we obtain

`\begin{gathered} 5-15=10\sin (2\pi(t-(1)/(4))-2\pi) \\ \text{then} \\ 10\sin (2\pi(t-(1)/(4))-2\pi)=-10 \end{gathered}`

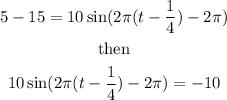
By moving the coefficient 10 the the right hand side, we get

`\begin{gathered} \sin (2\pi(t-(1)/(4))-2\pi)=-(10)/(10) \\ \sin (2\pi(t-(1)/(4))-2\pi)=-1 \end{gathered}`

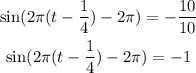
we can note that when

`\sin \theta=-1\Rightarrow\theta=-90=-(\pi)/(2)`

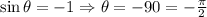
this implies that the argument of our last result is

`2\pi(t-(1)/(4))-2\pi=-(\pi)/(2)`

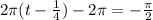
By moving 2Pi to the right hand side, we have

`\begin{gathered} 2\pi(t-(1)/(4))=-(\pi)/(2)+2\pi \\ 2\pi(t-(1)/(4))=(3\pi)/(2) \end{gathered}`

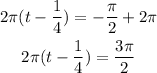
Now, by moving 2Pi to the right hand side, we have

`t-(1)/(4)=-((3\pi)/(2))/(2\pi)`

which gives

`t-(1)/(4)=(3)/(4)`

so, t is given by

`\begin{gathered} t=(3)/(4)+(1)/(4) \\ t=1 \end{gathered}`

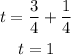
That is, n 1 minute, the car will take one full rotation.

c) The maximum height of the car ocurrs at t=0.5 min because in one minute it take one full rotation. Then, at t=1/2 we get

`H((1)/(2))=10\sin (2\pi((1)/(2)-(1)/(4)))+15`

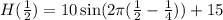
which gives

`\begin{gathered} H((1)/(2))=10\sin (2\pi((1)/(4)))+15 \\ H((1)/(2))=10\sin ((\pi)/(2))+15 \\ H((1)/(2))=10(1)+15 \\ H((1)/(2))=25 \end{gathered}`

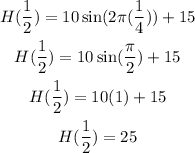
that is, the maximum height is 25 feets