Question

Consider the equation x 2+ 1 = 7-x

Answer 1

Since the given equation is

`x^2+1=7-x`

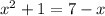
Since (-3, 2) is its solution which means the graphs of each side are intersected at point (-3, 2)

To verify the solution, substitute x by -3 on each side

If the two sides are equal, then the point is the solution to it

`\begin{gathered} L\mathrm{}H\mathrm{}S=x^2+1 \\ x=-3 \\ L\mathrm{}H\mathrm{}S=(-3)^2+1 \\ L\mathrm{}H\mathrm{}S=9+1 \\ L\mathrm{}H\mathrm{}S=10 \end{gathered}`

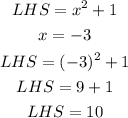
Let us do the same with the right-hand side

`\begin{gathered} R\mathrm{}H\mathrm{}S=7-x \\ x=-3 \\ R\mathrm{}H\mathrm{}S=7-(-3) \\ R\mathrm{}H\mathrm{}S=7+3 \\ R\mathrm{}H\mathrm{}S=10 \end{gathered}`

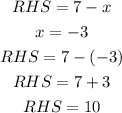
L.H.S = R.H.S = 10

This means the value of y = 10, not 2

Then (-3, 2) is not a solution of the given equation

Now we will draw each side, then find the point of intersection between them

From the graph, the solutions are the intersection points between the line and the graph

The two points are (-3, 10) and (2, 5)