Question

Trent decided bicycle to Austin and back. Hisaverage speed to Austin was 45 km/h. The averagespeed on his return trip was 30 km/h. The trip toAustin was 1 hour less than his time bicycling on hisreturn trip. How many hours did the trip to Austinlake?

Answer 1

Consider the relation,

`\text{Time}=\frac{\text{ Distance}}{\text{ Speed}}`

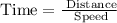
Let the distance between Trent and Austin is 'd' kilometers.

Then the time taken by Trent to reach Austin is given by,

`T_1=(d)/(45)`

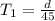
Similarly, the time taken by Trent on his return trip is given by,

`T_2=(d)/(30)`

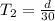
Given that the trip to Austin was 1 hour less than the return trip,

`\begin{gathered} T_2-T_1=1 \\ (d)/(30)-(d)/(45)=1 \\ d((1)/(30)-(1)/(45))=1 \\ d((45-30)/(30*45))=1 \\ d=(30*45)/(15) \\ d=2*45 \\ d=90 \end{gathered}`

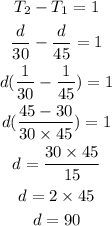
Solve for the total time of the trip as,

`\begin{gathered} T=T_1+T_2 \\ T=(90)/(45)+(90)/(30) \\ T=2+3 \\ T=5 \end{gathered}`

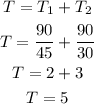
Thus, the total time required for complete trip is 5 hours.