Given: The velocity function of a moving particle as
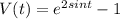
To Determine: The time at which the acceleration equals to zero
Solution
Note that at time t=0, the particle is at origin, so
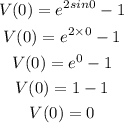
Determine the acceleration function
The acceleration of a particle is the rate of change of velocity or the derivative of the velocity function. Therefore,
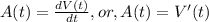
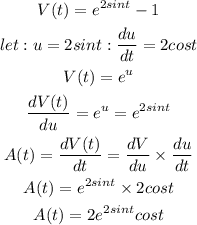
When the acceleration is equal to zero, then we have
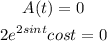
Let us plot the graph of the acceleration function
The time for given interval for which the acceleration is zero are
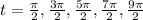
ence, thre first time the acceleration is zero is π/2 or 1.571