Question

Help me with question 2, thank you!

Answer 1

Given the function f(x):

`f(x)=3x^2-5x-4`

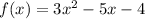
We will find the point on the given parabola where the slope of the tangent is horizontal

The horizontal line has a slope = zero

The slope of the line is the first derivative of the function

So, we will find the first derivative and equate it to zero

`\begin{gathered} f^(\prime)(x)=0 \\ 3(2x)-5(1)-(0)=0 \end{gathered}`

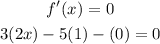
solve the equation to find (x):

`\begin{gathered} 6x-5=0 \\ 6x=5 \\ x=(5)/(6) \end{gathered}`

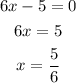
substitute with the value of (x) into the given function to find the y-coordinate

`y=3((5)/(6))^2-5((5)/(6))-4=(-73)/(12)`

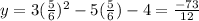
So, the answer will be the point will be as follows:

`(x,y)=((5)/(6),(-73)/(12))`

See the following figure: