Solution:
Given the a figure;
The figure is a square with the unshaded region is a semi circle.
The measure of the side lengths of the square is 25 ft
To find the area, A, of the shaded region, the formula is
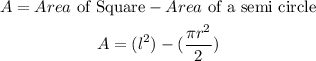
Where
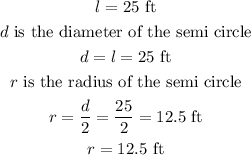
Substitute the values of the variables into the formula above
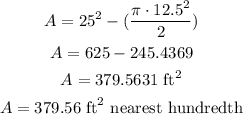
Hence, the answer is 379.56 ft² (nearest hundredth)