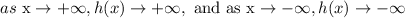Question

Graph the polynomial function. Note x- and y-intercepts, multiplicity, and end behavior.h(x) = (x − 1)3(x + 2)2

Answer 1

Given:

`h\left(x\right)=\left(x-1\right)^3\left(x+2\right)^2`

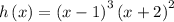
To graph the given polynomial function, we can plug in any values of x to find values of h(x). The graph is shown below:

We also note that the x-intercept is the point on the x-axis, while the y-intercept is the point on the y-axis. Hence,

x-intercepts: (1,0), (-2,0)

y-intercept: (0,-4)

Tt can also be noted that (x − 1) occurs 3 times while (x+2) occurs 2 times. Hence, x=1 has a multiplicity 3, while x=-2 has a multiplicity 2.

aased on the graph, the end behavior would be:

`as\text{ x}\rightarrow+\infty,h(x)\rightarrow+\infty,\text{ and as x}\rightarrow-\infty,h(x)\rightarrow-\infty`