Question

What is this equation rewritten in the form that reveals the minimum of the function

Answer 1

We are given the quadratic function c(p) = p^2 - 28p + 250 and we need to rewrite this in such a way that the minimum value is easy to find.

Remember that the vertex

`f(x)=a(x-h)^2+k`

where (h, k) is the vertex or the minimum point.

We use completing the squares method to do this. We divide the second term, -28p, by 2p, then square it.

`((-28p)/(2p))^2=(-14)^2=196`

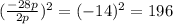
We add 196 to p^2 - 28p to make it equal to (p - 14)^2, but since it will change the value of the equation, we need to subtract the same value from 250 so that the net effect is zero.

`\begin{gathered} c(p)=p^2-28p+250 \\ c(p)=(p^2-28p+196)+250-196 \\ c(p)=(p-14)^2+54 \end{gathered}`

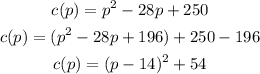
The equation is c(p) = (p - 14)^2 + 54.