Question

Let -3 -5 be a point on the terminal

Answer 1

We have a terminal point (-3,-5).

We have to find cos(θ), csc (θ and tan)(θ.)

We can locate the terminal point and the angle as:

The cosine of this angle will be negative, as ( is located in the third quadrant)

The hypotenuse of this right triangle will be called R and we can calculate it using the Pythagorean theorem:

`\begin{gathered} R^2=x^2+y^2 \\ R=\sqrt[]{x^2+y^2} \end{gathered}`

We can estimate the cosine as:

`\begin{gathered} \cos (\theta)=(x)/(R) \\ \cos (\theta)=\frac{-3}{\sqrt[]{(-3)^2+(-5)^2}} \\ \cos (\theta)=\frac{-3}{\sqrt[]{9+25}} \\ \cos (\theta)=\frac{-3}{\sqrt[]{34}} \\ \cos (\theta)=\frac{-3\sqrt[]{34}}{34} \end{gathered}`

We can now relate this to the csc(θ) as:

`\begin{gathered} \csc (\theta)=(1)/(\sin (\theta)) \\ \csc (\theta)=(1)/((y)/(R)) \\ \csc (\theta)=(R)/(y) \\ \csc (\theta)=\frac{\sqrt[]{34}}{-5} \\ \csc (\theta)=-\frac{\sqrt[]{34}}{5} \end{gathered}`

Finally, we can calculate the tangent as:

`\begin{gathered} \tan (\theta)=(y)/(x) \\ \tan (\theta)=(-5)/(-3) \\ \tan (\theta)=(5)/(3) \end{gathered}`

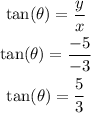
Answer:

cos(θ) = -3√34/34

csc(θ) = -√34/5

tan(θ) = 5/3