Given:
The car ride from Kiley's house to the airport.
Distance =24.3 miles.
Time =1/2 hour.
We know that

Substitute Distance =24.3 miles and time =1/2 hour to compute the average rate of the car ride from Kiley's house to the airport.
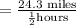
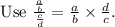
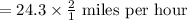
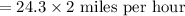
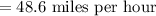
Hence the average rate of the car ride from Kiley's house to the airport is 48.6 miles per hour.
2)
Given that they walked 3/4 hours to the waiting area and covered the distance of 1.2 miles.
Distance =1.2 miles.
Time =3/4 hours.
we know that

Substitute distance =1.2 miles and time =3/4 hours to compute the average rate of the walk from the car to the waiting area by the gate, at the airport.
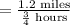

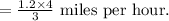
Multiplying 1.2 and 4, we get 4.8
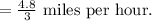
Dividing 4.8 by 3, we get 1.6
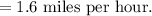
Hence at the airport, the average rate of the walk from the car to the waiting area by the gate is 1.6 miles per hour.