Question

Line segments JK and JL in the xy-coordinate plane both have a common endpoint /(-4, 11) andmidpoints at M, (2,16) and M, (-3, 5), respectively.What is the distance between M, and M.? Round to the nearest tenth

Answer 1

From the question, since the coordinates of the mid-points JK and JL has been given as M (2,16) and M, (-3, 5), respectively.

To find the distance between these two mid-points, we simply use the distance formula to do that.

The distance formula is given as

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ where\text{ d is the distance } \end{gathered}`

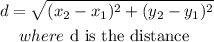
Applying these to the points M (2,16) and M, (-3, 5), we have

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=√((-3-2)^2+(5-16)^2) \\ d=√((-5)^2+(-11)^2) \\ d=√(25+121) \\ d=√(146) \\ d=12.083045 \\ d=12.1\text{ units } \end{gathered}`

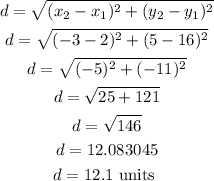
Hence the answer is 12.1 units