Question

I need help with the whole question

Answer 1

Given:

`\begin{gathered} f(x)=2x^2-4x-6 \\ g(x)\text{ = 3x-4} \\ h(x)\text{ = }(2)/(x) \\ \end{gathered}`

1.1.1 The equation of the reflection of g(x) in the x-axis is of the form:

The rule for the reflection in the x-axis:

`(x,y)\rightarrow\text{ (x,-y)}`

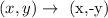
Applying the rule:

`\begin{gathered} g^(\prime)(x)\text{ = -g(x)} \\ =-(3x\text{ -4)} \\ =\text{ 4 -3x} \end{gathered}`

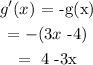
Hence, g'(x) = 4-3x

1.1.2 The equation of the reflection of h(x) in the y-axis.

The rule for reflection in the y-axis:

`(x,y)\rightarrow\text{ (-x,y)}`

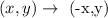
Applying the rule:

`h^(\prime)(x)\text{ = }(2)/(-x)`

Hence, h('x) = 2/-x

1.1.3 The values of k for which :

`k=2x^2-4x-6`

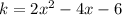
Re-arranging:

`\begin{gathered} 2x^2-4x-6-k\text{ =0} \\ 2x^2-4x\text{ -(6+k) = 0} \end{gathered}`

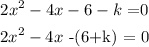
Using the rule that for an equation to have non-real roots, the discriminant (D) must be less than zero.

`\begin{gathered} D=b^2-4ac \\ (-4)^2\text{ -4(2)-(6+k) }<\text{ 0} \end{gathered}`

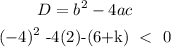
Simplifying we have:

`\begin{gathered} 16\text{ +48+8k }<\text{ 0} \\ 64\text{ + 8k }<\text{ 0} \\ 8k\text{ }<\text{ -64} \\ \text{Divide both sides by 8} \\ (8k)/(8)\text{ }<(-64)/(8) \\ k\text{ }<\text{ -8} \end{gathered}`

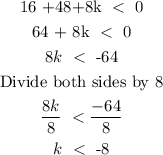
Hence, the values of k for which the equation has non-real roots is that k must be less than -8

1.1.4 The average gradient of f(x) between x=-4 and x=0:

First, we need to find the value of f(x) at x=-4.

`\begin{gathered} f(-4)=2(-4)^2\text{ -4(-4) -6} \\ =\text{ 32+16 -6} \\ =\text{ 42} \end{gathered}`

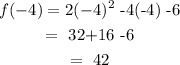
Next, we must find the value of f(x) at x=0:

`\begin{gathered} f(0)=2(0)^2-4(0)\text{ -6} \\ =\text{ -6} \end{gathered}`

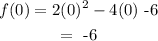
Using the average gradient formula:

`\begin{gathered} \text{Average gradient = }(y_B-y_A)/(x_B-x_A) \\ =\text{ }(-6-42)/(0-(-4)) \\ =(-48)/(4) \\ =\text{ -12} \end{gathered}`

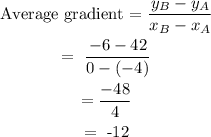
Hence, the average gradient is -12