Question

Can someone help me please

Answer 1

Given,

The distance of the race, d=100 m

The extended distance of the race, s=200 m

The velocity of the red car throughout the race, u₁=10 m/s

The initial velocity of the blue car, u₂=0 m/s

The blue car gains a velocity of 2 m/s every second.The constant acceleration of the blue car is

hus t

`\begin{gathered} a=(2)/(1) \\ =2\text{ m/s}^2 \end{gathered}`

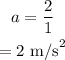
As the red car maintains the same velocity, the speed when it reaches the finish line will be 10 m/s.The time it takes for the red car to reach the finish line when the race was 100 m

`(t_1)_(100)=(d)/(u_1)`

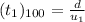
On substituting the known values,

`\begin{gathered} (t_1)_(100)=(100)/(10) \\ =10\text{ s} \end{gathered}`

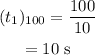
The time it takes for the red car to reach the finish line after the race is extended,

`(t_1)_(200)=(s)/(u_1)`

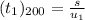
On substituting the known values,

`\begin{gathered} (t_1)_(200)=(200)/(10) \\ =20\text{ s} \end{gathered}`

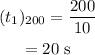
From the equation of motion,

The final velocity of the blue car, when it reaches the finish line of 100 m race is given by the equation of motion,

`v^2_(100)=u^2_2+2ad`

Where v₁₀O is the final velocity of the blue car at the end of the 100 m race.n substituting the known values,₀

`\begin{gathered} v^2_{^{}100}=0+2*2*100 \\ =400 \\ v=\sqrt[]{400} \\ =20\text{ m/s} \end{gathered}`

hus the speed of the blue car when it reaches the finish line of 100 m race is 20 m/s

he time it takes for the blue car to reach the end of the 100 m race is given by,

`v_(100)=u_2+a(t_2)_(100)`

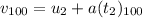
Where (t₂)₁₀₀ is the time it takes for the blue car to reach the end of the 100 m race.

On substituting the known values in the above equation,

`\begin{gathered} 20=0+2(t_2)_(100) \\ \Rightarrow(t_2)_(100)=(20)/(2) \\ =10\text{ s} \end{gathered}`

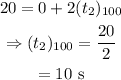
hus both cars take 10 s to reach the end of the 100 m race. Thus they both reach the finitsh line together.

The time it takes for the blue car to reach the end of the 200 m race can be calculated using the equation,

`s=u_2(t_2)_(200)+(1)/(2)a\lbrack(t_2)_(200)\rbrack^2`

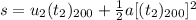
Where (t₂)₂₀₀ is the time it takes for the blue car to reach the end of the 200 m race.

On substituting the known values,

`\begin{gathered} 200=0+(1)/(2)*2*\lbrack(t_2)_(200)\rbrack^2 \\ \lbrack(t_2)_(200)\rbrack^2=200 \\ \Rightarrow(t_2)_(200)=\sqrt[]{200} \\ =14.14\text{ s} \end{gathered}`

hus while rthe ed car takes 200 s to reach the finish line of the 200 m race, the blue car takes 14.14 s.

Therefore, if the race was extended, the blue car will reach the finish line first.