The perimeter is the sum of all the sides of a geometric figure, so
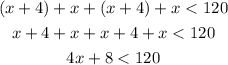
To resolve this inequality you can first subtract 8 from both sides
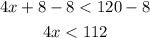
Then you divide by 4 on both sides of the inequality

Therefore, for the perimeter of the rectangle to be less than 120, its shortest side must measure less than 28.