From the given equation :
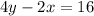
This can be written in the slope-intercept form :

where m is the slope
and b is the y-intercept
Rewriting the equation :
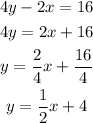
The equation will be y = 1/2 x + 4
the slope is m = 1/2
nd the y-intercept is b = 4
Note that parallel lines have the same slope.
So the slope of parallel line is m = 1/2
Perpendicular lines have a slope of negative reciprocal with each other.
So the slope of perpendicular line to this line is m = -2
Equation of parallel line :
we have :
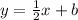
Let's say the line passes at the origin (0, 0)
If a line passes thru the origin, the y-intercept is always b = 0
Therefore, the equation of parallel line is y = 1/2 x
quation of perpendicular line :
we have :
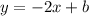
Let's also say that the line passes at the origin (0, 0)
and the y-intercept is also b = 0
he equation of the perpendicular line is yy = -2x
raphing these equations will be :
Original line (Blue)
Parallel line (Orange)
Perpendicular line (Pink)
y-intercepts :
(0, 0) and (0, 4)