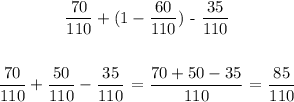Question

Of a company’s 110 employees. 70 work full time and 60 are married. Half of the full time workers are married. b. What is the probability that an employee works full-time or is married?P(full-time) OR (Married) - P(full-time and married)c. What is the probability than an employee works full-time or is not married?P(full-time) OR P(Not Married) - P(full-time and not married)

Answer 1

nswer:

Step-by-step explanation:

) We want to start by drawoing a Venn diagram

We call the set of the married people M and the set of the full-time workers F

We have the Venn diagram represented as follows:

b) We want to get the probability that an employee works full time and is married

We have that as:

P(full-time) OR P(married) -P(Full time and married)

P(full time) = 70/110

P(married) = 60/110

P(full time and married) = 35/110 (since half of the full-time workers are married)

Thus, we have:

:

`(70)/(110)+\text{ }(60)/(110)-(35)/(110)\text{ = }(95)/(110)`

c) The probability that an employee works full time or is not married

Mathematically, we have that as:

P(full time) OR P(not married) -P(full time and not married)

P(not married) = 1 - P(married)

:

`\begin{gathered} (70)/(110)+(1-(60)/(110))\text{ - }(35)/(110) \\ \\ (70)/(110)+(50)/(110)-(35)/(110)\text{ = }(70+50-35)/(110)\text{ = }(85)/(110) \end{gathered}`