SOLUTION
Step1:
hence from the diagram above, the dimension of the rug is
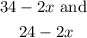
Since we have area of the rug,
then we have
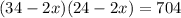
We now solve the equation above quadratically
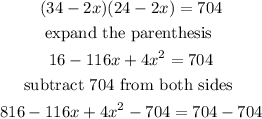
Then we have

Solve using factor method we obtain
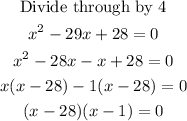
Equating each factor to zero we have
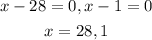
Since x can not be 28, the value of x is 1
The Dimension of the rug becomes
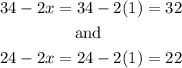
Hence the dimension of the rug is 32 ft by 22ft (22,32)