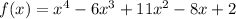Question

Need help, please.Quick answer is okay

Answer 1

xplanation:

Step 1. e are given the following zeros of a polynomial function.

- 1 with a multiplicity of two, which means that is a zero two times:

`\begin{gathered} x_1=1 \\ x_2=1 \end{gathered}`

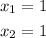
and the other two zeros are:

`\begin{gathered} x_3=2+√(2) \\ x_4=2-√(2) \end{gathered}`

And we need to find the equation that has these four zeros.

tep 2. 2R

`f(x)=(x-x_1)(x-x_2)(x-x_3)(x-x_4)`

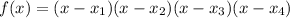
tep 3. S

`f(x)=(x-1)(x-1)(x-(2+√(2)))(x-(2-√(2)))`

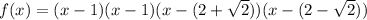
tep 4. S

`f(x)=(x-1)(x-1)(x-2-√(2))(x-2+√(2))`

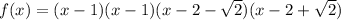
tep 5. T

`f(x)=(x^2-2x+1)(x-2-√(2))(x-2+√(2))`

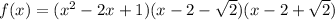
Then, let's multiply the second and third parentheses:

`f(x)=(x^2-2x+1)(x^2-2x+x√(2)-2x+4-2√(2)-x√(2)+2√(2)-2)`

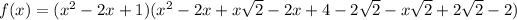
Multiple terms cancel and the result is:

`f(x)=(x^2-2x+1)(x^2-4x+2)`

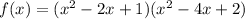
tep 6. TT

`f(x)=x^4-4x^3+2x^2-2x^3+8x^2-4x+x^2-4x+2`

Combining like terms:

`f(x)=x^4-6x^3+11x^2-8x+2`

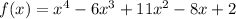
This is shown in option D.

Answer:

D

`f(x)=x^4-6x^3+11x^2-8x+2`