Question

Enter the values needed to find thelength CB. (Simplify your answer.)A(-3a, b)IFB(3a, b)ECB = V(4a)2 + ([?])2C(-a, -5b)Distance Formula: d = (x2 – xı)2 + (y2 - yı)2

Answer 1

We are asked to find the values needed for the length CB

The coordinates of points C and B are given as

C(-a, -5b)

Recall that the distance formula is given by

`d=\sqrt{\left( {x_2 - x_1 } \right)^2 + \left( {y_2 - y_1 } \right)^2 }`

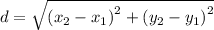
For the given case,

`\begin{gathered} (x_1,y_1)=\mleft(-a,-5b\mright) \\ (x_2,y_2)=\mleft(3a,b\mright) \end{gathered}`

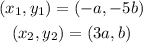
Let us substitute these coordinates into the above distance formula

`\begin{gathered} CB=\sqrt[]{({x_2-x_1})^2+({y_2-y_1})^2} \\ CB=\sqrt[]{({3a_{}-(-a)})^2+({b_{}-(-5b)_{}})^2} \\ CB=\sqrt[]{({3a_{}+a})^2+({b_{}+5b})^2} \\ CB=\sqrt[]{({4a})^2+({6b})^2} \end{gathered}`

Therefore, the required values are

`CB=\sqrt[]{({4a})^2+({6b})^2}`