Question

A catering service offers 8 appetizers, 9 main courses, and 3 desserts. A customer is to select 6 appetizers, 6 main courses, and 2 desserts for a banquet. Inhow many ways can this be done?

Answer 1

Given:

Number of appetizers offered = 8

Number of appetizers customer is to select = 6

Number of main courses offered = 9

Number of main courses customer is to select = 6

Number of desserts offered = 3

Number of desserts the customer is to select = 2

Let's determine how many ways this can be done.

This is a combination problem.

To determine the number of ways this can be selected, apply the combination formula below:

`_nC_r=(n!)/(r!(n-r)!)`

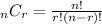
Thus, we have:

`_nC_r=_8C_6\ast_9C_6\ast_3C_2`

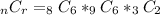
Solving further, let's apply the formula and combine:

`\begin{gathered} _8C_6\ast_9C_6\ast_3C_2=(8!)/(6!(8-6)!)\ast(9!)/(6!(9-6)!)\ast(3!)/(2!(3-2)!) \\ \\ _8C_6\ast_9C_6\ast_3C_2=(8!)/(6!(2)!)\ast(9!)/(6!(3)!)\ast(3!)/(2!(1)!) \end{gathered}`

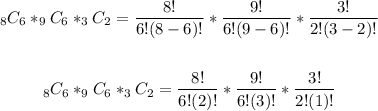
Solving further:

`\begin{gathered} _8C_6\ast_9C_6\ast_3C_2=(8\ast7\ast6!)/(6!(2\ast1))\ast(9\ast8\ast7\ast6!)/(6!(3\ast2\ast1))\ast(3\ast2!)/(2!(1)) \\ \\ _8C_6\ast_9C_6\ast_3C_2=(8\ast7)/(2\ast1)\ast(9\ast8\ast7)/(3\ast2\ast1)\ast(3)/(1) \\ \\ _8C_6\ast_9C_6\ast_3C_2=(56)/(2)\ast(504)/(6)\ast(3)/(1) \\ \\ _8C_6\ast_9C_6\ast_3C_2=28\ast84\ast3 \\ \\ _8C_6\ast_9C_6\ast_3C_2=7056 \end{gathered}`

herefore, there are