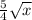Step-by-step explanation:
The question involves dividing radicals
To resolve the question, we will follow the steps below
Step 1: Write the expression
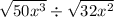
Step 2: simplify the expression in parts and apply the laws
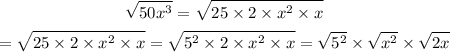
Thus
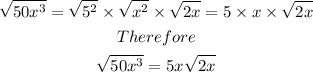
For the second part
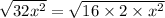
simplifying further
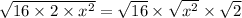
Hence, we have
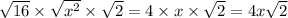
Finally, we will combine the simplified terms, so that we will have
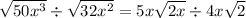
Hence, we will have
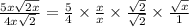
By canceling out the common parts, we will have the answer to be