A.
The length of the diagonal is given by the Pythagorean theorem therefore
![d=\sqrt[]{4^2+4^2}=\sqrt[]{16+16}=\sqrt[]{32}](https://img.qammunity.org/2023/formulas/mathematics/college/xtapzhe4w1d4n13u7afibz6f3pwfy5gbur.png)
The length of the diagonal is ) units
B.
The area of the square is given by the next formula
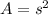
where s is the side
s=4
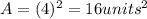
The area of the square is 16 units^2
C.
For the area of the triangle we will use the next formula
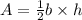
where b is the base and h is the height
b=4 units
h=4units
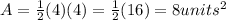
The area of the triangle formed by a diagonal and two of the sides is 8 units^2
D.
For the area of this triangle, we will use the same formula that we use in C. but in this case
b=sqrt(32)/2
h=sqrt(32)/2
We substitute the values
![A=(1)/(2)(\frac{\sqrt[]{32}}{2})(\frac{\sqrt[]{32}}{2}))=4units^2](https://img.qammunity.org/2023/formulas/mathematics/college/zvnct5evusx17t3unp6ivt58blboy8of4j.png)
The area of one of these triangles is 4 units^2
ANSWER
A. sqrt(32) units
B.16 units^2
C. 8 units^2
D. 4 units^2