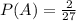Given
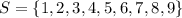
by selecting two numbers from S, the number of possible outcomes is
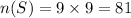
Let E be the event that selecting two numbers randomly and their sum is 12 with replacement.
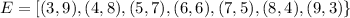
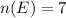
The probability is
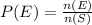
Substitute values, we get
h is
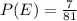
b)without replacement
Areplacementout
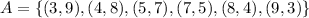
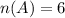
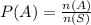
Substitute the values, we get
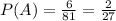
The probability that the sum is 12 if selecting two numbers without replacement