SOLUTION
Given the question in the image, the following steps can be used to get x
Step 1: Explain the concept of equal arcs in a circle
If a circle is divided into arcs, then each arc is a minor arc and they all sum up to be equal to the total angles in the circumfference of the circle which is 360 degrees.
Step 2: Explain the breakdown of the minor arcs in the circle
It can be seen that the minor arcs divided the circle into three parts which are two equal arcs and a 70 degrees arc. This implies that:
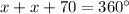
Step 3: Find x
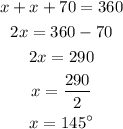
Hence, the value of x in the given circle is 145 degrees