Question

Find the missing side. Round answer to the nearest tenth.46°X145.910.10 0 0 013.219.5

Answer 1

Given the rigth triangle, you have to determine the length of the missing side marked with an x.

To do so you have to apply the trigonometric functions, these are calculated as:

`\begin{gathered} \sin \theta=\frac{opposite}{\text{hypotenuse}} \\ \cos \theta=(adjacent)/(hypotenuse) \\ \tan \theta=(opposite)/(adjacent) \end{gathered}`

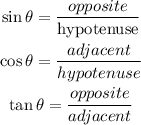
Where

θ is one of the inner angles of the triangle.

"opposite" indicates the opposite side to than angle

"adjacent" is the side in contact or next to the angle

and "hypotenuse" is the longest side of the triangle.

In this exercise we know the measure of the angle and the hypotenuse, the trigonometric function you have to use to determine the length of "x" is the Sine:

`\begin{gathered} \sin \theta=(opposite)/(hypotenuse) \\ \text{opposite}=\sin \theta\cdot hypotenuse \end{gathered}`

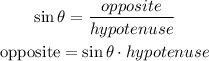
Replace with:=46º

hypotenuse=14

opposite=x

`\begin{gathered} x=\sin 46\cdot14 \\ x=10.07\cong10.1 \end{gathered}`

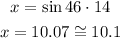
Correct option is b. 10.1