Answer:
(a) {-1, 1)
(b) {-11}
(c) {-3, 4}
***(d) { x < -1 or x > 1, I am not sure how else to put it, try {-1, 1} if you are not allowed to put in > or < signs
(e) (-∞, -11] or x ≤ -11
(f) {-3, 4}
(g) ( -√2, √2)
***I know the correct solution sets but I am not sure how to represent all of them given the one box you have in your solution for (a). Maybe the solution boxes for the other parts are different. Without knowing that I am only able to provide what is the correct expression
Explanation:
We have
f(x) = x² - 1
g(x) = x + 11
(a) f(x) = 0
=> x² - 1 =
=> x² = 1
x = ± 1
Answer (a): The solution set is {-1, 1}
(b)
g(x) = 0
=> x + 11 = 0
=> x = -11
Answer (b): Solution set: {-11}
(c)
f(x) = g(x)
=> x² - 1 = x + 11
=> x² -x -12 = 0
This is a quadratic equation which can be solved by factoring:
=> (x - 4)(x+3) = 0
=> x = 4, x = -3
{-3, 4} Answer
(d) f(x) > 0
=> x² - 1 > 0
Add 1 to both sides
x² > 1
x < -1 or x > 1
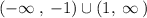
(e) g(x) ≤ 0
=> x + 11 ≤ 0
=> x ≤ -11
{-∞, -11}
(f)f(x) > g(x)
=> x²-1 > x +11
=> x² -x - 12 > 0
=> (x + 3)(x +4) > 0
=> x + 3 >0 and x - 4 > 0
=> x > -3 and x < 4
{-3, 4}
(g) f(x) ≥ 1
=> x² - 1 ≥ 1
=> x² ≥ 2
=> x ≥ ± √2
=> x ≤ -√2 or x ≥ √2
=> { -√2, √2}
In the above derivations note that if x² ≥ 1 then two possibilities are
x < - 1 or x > 1