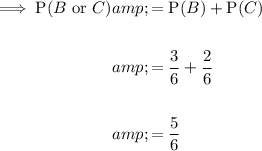Question

Need help on probability. Please explain how you did it so I can know how to do it.

Answer 1

I believe it should be 5/6

Explanation:

Here's why, the probability of getting a B, or an even number is 3/6 since there are 3 even numbers on a dice. The probability of getting a multiple of 3 is 2/6 since the only multiples of 3 are 1 and 3. Add the 2 together to get 5/6. Hope this helps.

Answer 2

`\text{P}(B \text{ or }C)=(5)/(6)`

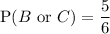
Explanation:

Mutually Exclusive Events

For two events, A and B, where A and B are mutually exclusive:

`\boxed{\text{P}(A \text{ or }B)=\text{P}(A)+\text{P}(B)}`

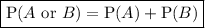
Probability distribution table:

`\begin{array}c\cline{1-7} x & 1 & 2 & 3 & 4 & 5 & 6 \\\cline{1-7} \text{P}(X=x)\phantom{\frac11}&(1)/(6)&(1)/(6)&(1)/(6)&(1)/(6)&(1)/(6)&(1)/(6)\\\cline{1-7}\end{array}`

where X is the score on a fair, six-sided dice.

P(B or C) means "the probability of rolling an even number or a multiple of 3".

As an even number of a fair, six-sided dice can never be a multiple of 3, the two events B and C are mutually exclusive.

Calculate the probabilities for events B and C.

Event B

Rolling an even number.

`\begin{aligned}\implies \text{P}(X \text{ is even})&=\text{P}(2 \text{ or }4\text{ or }6)\\\\&=\text{P}(X=2)+\text{P}(X=4)+\text{P}(X=6)\\\\& = (1)/(6)+ (1)/(6)+ (1)/(6)\\\\&=(3)/(6)\end{aligned}`

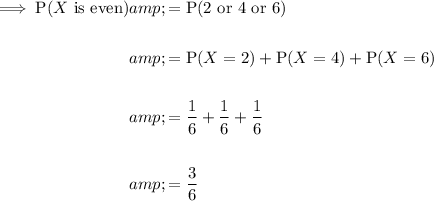
Event C

Rolling a multiple of 3.

`\begin{aligned}\implies \text{P}(X \text{ is multiple of 3})&=\text{P}(3 \text{ or }6)\\\\&=\text{P}(X=3)+\text{P}(X=6)\\\\& = (1)/(6)+ (1)/(6)\\\\&=(2)/(6)\end{aligned}`

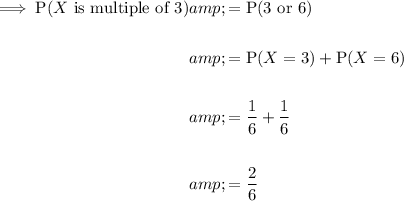
Solution

`\begin{aligned}\implies \text{P}(B \text{ or }C)&=\text{P}(B)+\text{P}(C)\\\\& = (3)/(6)+(2)/(6)\\\\& = (5)/(6)\end{aligned}`