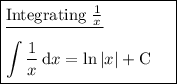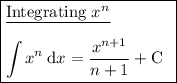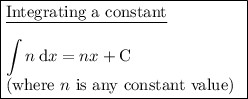Answer:
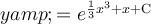
Explanation:
Given differential equation:
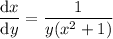
Rearrange the equation so that all the terms containing y are on the left side, and all the terms containing x are on the right side:
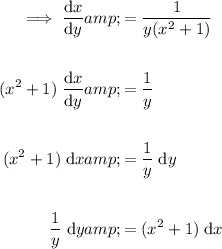
Integrate both sides:
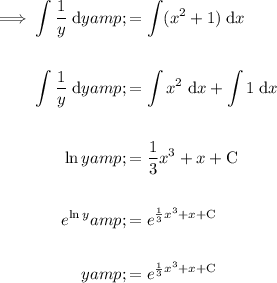
Therefore, the solution to the given differential equation is:
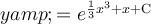
Integration rules used: