Question

Answer 7 and 10 only​

Answer 1

7.
We are given:
abcissa(x-coordinate) of given point: -6
let's say the ordinate(y-coordinate) of the given point is y
distance of the given point from (1,3) = √74

we can rewrite the given information as:
the distance between the points (-6,y) and (1,3) is √74

finding y:
we know that in order to find the distance between any two points, we use the distance formula, which goes as follows:
distance =
`√((x_1-x_2)^2 + (y_1 - y_2)^2)`

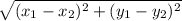
from the data we are given, let's say that:
(x₁, y₁) = (-6, y)
(x₂, y₂) = (1, 3)
(you can use them interchangably, there is no restriction on which point gets to be labelled as 1)

plugging this in the distance formula, we get:
distance =
`√((-6-1)^2 + (y - 3)^2)`
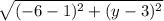
we are also given that the distance is √74,

√74 =
`√((-7)^2 + (y - 3)^2)`

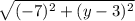
squaring both sides to get rid of the square root

74 = (-7)² + (y - 3)²
74 = 49 + y² + (3)² -2(y)(3) (using the "square of sum" identity)
74 = 49 + y² + 9 - 6y
74 = 58 + y² - 6y
y² - 6y + 58 - 74 = 0 (subtracting 74 from both sides)
y² - 6y - 16 = 0
y² - 8y + 2y - 16 = 0 (splitting the middle term)
y(y - 8) + 2(y - 8) = 0
(y + 2)(y - 8) = 0
which means that:
y + 2 = 0 , y - 8 = 0
y = -2 , y = 8
These are the two possible values of y

8.
We are given:
points A and B
A: (3, y)
B: (6, 2)
distance between A and B = 5 units
finding possible values of y
here, we will use the distance formula again to find the value of y
distance formula:
`√((x_a-x_b)^2 + (y_a - y_b)^2)`
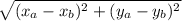
plugging the given values, we get:
5 =
`√((3-6)^2 + (y - 2)^2)`
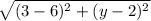
25 = (3 - 6)² + (y - 2)² (squaring both sides)
25 = (-3)² + (y - 2)²
25 = 9 + y² + (2)² - 2(y)(2)
25 = 9 + y² + 4 - 4y
y² - 4y + 9 + 4 - 25 = 0 (subtracting 25 from both sides)
y² - 4y - 12 = 0
y² - 6y + 2y - 12 = 0 (splitting the middle term)
y(y - 6) + 2(y - 6) = 0
(y + 2)(y - 6) = 0

y + 2 = 0 , y - 6 = 0
y = - 2 , y = 6
These are the two possible values of y