Main Answer:
Step-by-step explanation:
Given that,
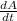 = -4
= -4
The surface area of the snow ball = 4π
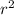
Let the surface area = A
If A denotes the surface area and D the diameter then,
A = 4π
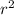 = 4π
= 4π
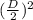
⇒ A = π
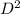
Differentiate with respect to r,
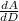 = 2πD
= 2πD
By using chain rule,
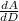 =
=
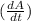
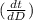 =
=
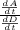
⇒ 2πD =
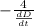
∴
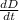 =
=
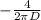
when D = 9,
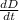 =
=
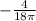
∴
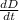 =
=
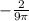
so, the diameter is decreasing at a rate of
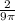 .
.