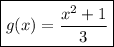Question

F(x) = 3x-1 , (f of g)(x) = x^2 , Find g(x)

Answer 1

`g(x)=(x^2+1)/(3)`

Explanation:

Given functions:

`\begin{cases}f(x)=3x-1\\(f \circ g)(x)=x^2\end{cases}`

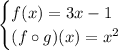
Composite functions are when the output of one function is used as the input of another.

Therefore, the given composite function (f o g)(x) means to substitute function g(x) in place of the x in function f(x).

`\begin{aligned}(f \circ g)(x) & = x^2\\f(g(x)) & = x^2\\\implies 3(g(x))-1 & = x^2\\3(g(x))-1+1 & = x^2+1\\3(g(x))&=x^2+1\\(3(g(x)))/(3)&=(x^2+1)/(3)\\\implies g(x)&=(x^2+1)/(3)\end{aligned}`

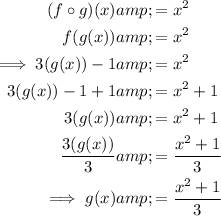
Therefore:

`\boxed{g(x)=(x^2+1)/(3)}`