Answer:
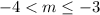
=========================================================
Reason:
If m = -4, then f(x) = m becomes f(x) = -4. This yields the single solution x = -4
How do we get this solution? Start at -4 on the y axis. Move horizontally until reaching the curve. You should arrive at (-4,-4) which is the lowest point of this curve. Then move upward until reaching the x axis to arrive at x = -4
All of this says that the input x = -4 leads to the output y = f(x) = -4
---------------
We've gone over m = -4 leading to one solution, so that's out of the question since we want two solutions.
But if m = -3 for instance, then notice how tracing a horizontal line to the curve arrives at two locations instead of one. We arrive at x = -2 and x = -5 as the solutions to f(x) = -3
All of these solutions mentioned are negative which fits the criteria we're after. If m is in the interval from -4 to -3, excluding -4 but including -3, then we'll have f(x) = m with two negative solutions for x.