Question

Help meeeeee plssss with steps​

Answer 1

p = 18, q = 0

Explanation:

The expression on the left side of the equation is

`\large \text {$ (√(5)+\:2)/(√(5)-2)+(√(5)-\:2)/(√(5)+2) $}`

Multiply the denominators to get a common denominator:

`\text{$\left(√(5)-2\right)\left(√(5)+2\right)$}`

=
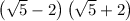
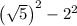`\left(√(5)\right)^2-2^2` ∵ (a + b)(a - b) = a² - b²

`=5-4\\\\= 1`

`\large \text {$ (√(5)+\:2)/(√(5)-2)+(√(5)-\:2)/(√(5)+2) $}\\\\`

`=(\left(√(5)+2\right)\left(√(5)+2\right))/(\left(√(5)-2\right)\left(√(5)+2\right)) + (\left(√(5) - 2\right)\left(√(5) - 2\right))/(\left(√(5)-2\right)\left(√(5)+2\right))`

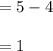
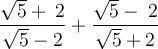
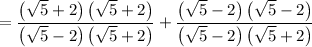
Since denominator

`\text{$\left(√(5)-2\right)\left(√(5)+2\right)$} = 1,`

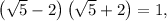
the expression becomes

`=\left(√(5)+2\right)^2 + \left(√(5)-2\right)^2\\\\= 5 + 4√(5) + 4 + 5 - 4√(5) + 4\\\\`

`= 10 + 8 = 18`

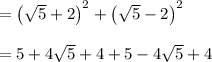
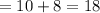
Therefore

`\large \text {$ (√(5)+\:2)/(√(5)-2)+(√(5)-\:2)/(√(5)+2) = p + q√(5)$}\\\\\\= > \large \text{$ 18 = p + q√(5)$}`

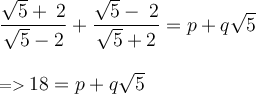
Now
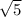`√(5)` is an irrational number and p = rational so since there is no
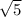`√(5)` term on the left side, q = 0 and p = 18