Answer:
1 Greatest Common Factor
We have to find out the greatest common factor, of the given polynomial to factorise it. This process is nothing but a type of reverse procedure of distributive law.
2. Grouping
This method is also said to be factoring by pairs. Here, the given polynomial is distributed in pairs or grouped in pairs to find the zeros.
3. Using Identities
The factorisation can be done also by using algebraic identities. The most common identities used in terms of the factorisation are:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
a2 – b2= (a + b)(a – b)
4. Zero Factor Property :The Zero Factor Property (also called the Zero Product Property) says that if the product of two quantities is zero, then at least one of those quantities is zero. The only way to get a product equal to zero is to multiply by zero itself.
5. Greatest Common Factor (GCF) Method:
This is almost always the first method applied to factoring polynomials. Look at all of the terms and see if they all have something in common that can be removed.
6. Sum or Difference in Two Cubes
A cube is a term that has been multiplied by itself twice.
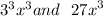
are all cubed terms. The trick to remembering how to factor cubed terms is S.O.A.P. S = same sign, O = opposite sign A.P. = always positive.