Answer:
see explanation
Explanation:
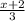 -
-
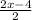 = 0
= 0
multiply through by 6 ( the LCM of 3 and 2 ) to clear the fractions
2(x + 2) - 3(2x - 4) = 0 ← distribute parenthesis on left side and simplify
2x + 4 - 6x + 12 = 0
- 4x + 16 = 0 ( subtract 16 from both sides )
- 4x = - 16 ( divide both sides by - 4 )
x = 4
------------------------------------------------------------
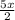 +
+
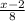 = 2 ( multiply through by 8 to clear the fractions )
= 2 ( multiply through by 8 to clear the fractions )
4(5x) + x - 2 = 16
20x + x - 2 = 16
21x - 2 = 16 ( add 2 to both sides )
21x = 18 ( divide both sides by 21 )
x =
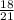 =
=

-----------------------------------------------------------
 -
-
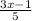 = -
= -

multiply through by 20 ( the LCM of 4, 5, 2 ) to clear the fractions
5(x - 5) - 4(3x - 1) = - 30 ← distribute parenthesis on left side and simplify
5x - 25 - 12x + 4 = - 30
- 7x - 21 = - 30 ( add 21 to both sides )
- 7x = - 9 ( divide both sides by - 7 )
x =

-------------------------------------------------------------
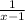 +
+
 =
=
 ← x² - 1 is a difference of squares , then
← x² - 1 is a difference of squares , then
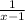 +
+
 =
=
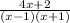
multiply through by (x - 1)(x + 1) to clear the fractions
x + 1 + x - 1 = 4x + 2
2x = 4x + 2 ( subtract 4x from both sides )
- 2x = 2 ( divide both sides by - 2 )
x = - 1
If we substitute this value back into the original equation, we find
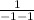 +
+
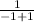 =
=

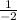 +
+
 =
=
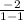
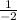 +
+
 =
=

division by zero is undefined
thus x = - 1 is an extraneous solution
the equation has no solution