Answer:
see explanation
Explanation:
1
1 +
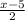 -
-
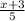 ≤ 0
≤ 0
multiply through by 10 ( the LCM of 2 and 5 ) to clear the fractions
10 + 5(x - 5) - 2(x + 3) ≤ 0 ← distribute parenthesis on left side and simplify
10 + 5x - 25 - 2x - 6 ≤ 0
3x - 21 ≤ 0 ( add 21 to both sides )
3x ≤ 21 ( divide both sides by 3 )
x ≤ 7
2
 -
-
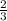 ≥ 4
≥ 4
multiply through by 15 ( the LCM of 5 and 3 ) to clear the fractions
18x - 10 ≥ 60 ( add 10 to both sides )
18x ≥ 70 ( divide both sides by 18 )
x ≥
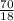 , that is
, that is
x ≥
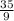
3
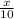 -
-
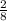 ≥ 1
≥ 1
multiply through by 40 ( the LCM of 10 and 8 ) to clear the fractions
4x - 10 ≥ 40 ( add 10 to both sides )
4x ≥ 50 ( divide both sides by 4 )
x ≥
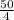 , that is
, that is
x ≥
