Answer:
j = 2
Explanation:
Slope of a line is given by:
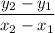
where (x₁, y₁) and (x₂, y₂) are two points on the line
This is commonly referred to as rise/run
Given the two points (6, 1) corresponding to (x₁, y₁) and (9, j) corresponding to (x₂, y₂)
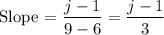
But we are given the slope as 1/3
So we get
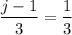
Multiplying by 2 on both sides gives us:
j - 1 = 1
Adding 1 to both sides gives us
j - 1 + 1 = 1 + 1
j = 2