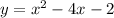Answer:
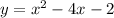
Explanation:
Standard Form of Quadratic:

Vertex Form of Quadratic:

h = vertex x
k = vertex y
Think of h and k as the ordered pair (h,k).
Match this ordered pair to the vertex ordered pair.
(h,k) = (2, -6)
Plug in (h,k) into vertex form:
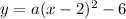
Use other point to solve for a.
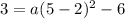
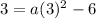
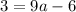
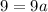
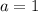
Plug a back into vertex form and expand the expression into standard form:
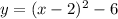
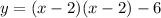
Use F.O.I.L. method to expand (x-2)(x-2).
F(first):

O(outer):
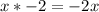
I(inner):
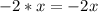
L(last):
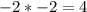
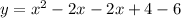
Combine like terms: