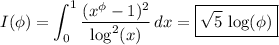Question

`\rm\int_0^1 \frac{( {x}^ \varphi - 1 {)}^(2) }{ log {}^(2) (x) } dx\\`​

Answer 1

I assume the natural logarithm, and not the base-10 log. Parameterize the integral as

`\displaystyle I(a) = \int_0^1 ((x^a - 1)^2)/(\log^2(x)) \, dx`

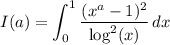
Differentiate twice with respect to
`a`.

`\displaystyle I'(a) = 2 \int_0^1 (x^(2a) -x^a)/(\log(x)) \, dx`

`\displaystyle I''(a) = 2 \int_0^1 (x^(2a) - x^a) \, dx`

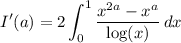
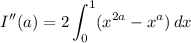
Evaluate the last integral, then solve for
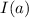`I(a)` with the fundamental theorem of calculus, noting that
`I(0)=I'(0)=0`.

`\displaystyle I''(a) = 2\left(\frac1{2a+1} - \frac1{a+1}\right)`

`\displaystyle I'(a) = 2 \int_0^a \left(\frac1{2t+1} - \frac1{t+1}\right) \, dt \\\\ ~~~~ = \log(2a+1) - 2 \log(a+1)`

`\displaystyle I(a) = \int_0^a (\log(2t+1) - 2\log(t+1)) \, dt \\\\ ~~~~ = (2a+1) \log(2a+1) - 2(a+1) \log(a + 1)`

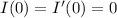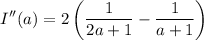
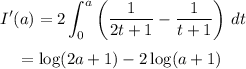
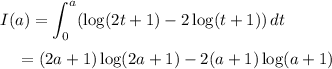
Let
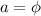`a=\phi` to recover the original integral.

`\displaystyle I(a) = (2\phi+1) \log(2\phi+1) - 2(\phi+1) \log(\phi + 1)`

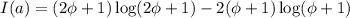
Using various properties of the golden ratio
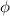`\phi`, namely

`\phi = 1 + \frac1\phi \implies \phi^2 = \phi + 1 \implies \phi^3 = \phi^2 + \phi`

`2\phi+1 = \phi\left(2+\frac1\phi\right) = \phi(1 + \phi)`

`\phi=\frac{1+\sqrt5}2 \implies \phi^3 = 2 + \sqrt5`

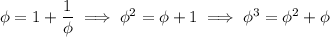
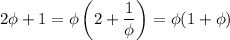
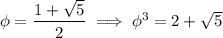
we can simplify the result to

`\displaystyle I(\phi) = \int_0^1 ((x^\phi-1)^2)/(\log^2(x)) \, dx = \boxed{\sqrt5\,\log(\phi)}`