Question

A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100

each month into an IRA earning 6% interest, how much will you have in the account after 20 years?

Answer 1

`~~~~~~~~~~~~\stackrel{\textit{payments at the end of the period}}{\textit{Future Value of an ordinary annuity}} \\\\ A=pmt\left[ \cfrac{\left( 1+(r)/(n) \right)^(nt)-1}{(r)/(n)} \right] \\\\\\ ~~~~~~ \begin{cases} A=\textit{accumulated amount}\\ pmt=\textit{periodic payments}\dotfill &100\\ r=rate\to 6\%\to (6)/(100)\dotfill &0.06\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{each months, thus twelve} \end{array}\dotfill &12\\ t=years\dotfill &20 \end{cases}`

`A=100 \left[ \cfrac{\left( 1+(0.06)/(12) \right)^(12 \cdot 20)-1}{(0.06)/(12)} \right] \\\\\\ A=100 \left[ \cfrac{\left( 1.005 \right)^(240)-1}{0.005} \right]\implies A \approx 46204.09`

Answer 2

After 20 years of depositing $100 each month into an IRA earning 6% interest, you will have approximately $44,494.52 in the account.

The amount you will have in the account after 20 years can be calculated using the formula for compound interest. In this case, you are depositing $100 each month into the IRA, and it is earning 6% interest.

To calculate the future value of the IRA after 20 years, you can break it down into smaller steps:

1. Calculate the monthly interest rate: Divide the annual interest rate by 12 months. In this case, the monthly interest rate is 6% / 12 = 0.5%.

2. Calculate the number of periods: Multiply the number of years by 12 months. In this case, 20 years * 12 months = 240 months.

3. Calculate the future value: Use the formula for compound interest, which is:

Future Value =
`P * ((1 + r)^n - 1) / r`

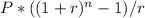
Where:
P is the monthly deposit ($100),
r is the monthly interest rate (0.5%),
n is the number of periods (240 months).

Plugging in the values into the formula, we get:

Future Value =
`100 * ((1 + 0.005)^240 - 1) / 0.005`

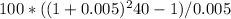
After evaluating this equation, you will find that the future value of the IRA after 20 years is approximately $44,494.52.