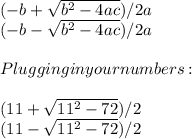Answer: x = 9, 2
Explanation:
I'm going to give you two main ways to solve this type of problem.
First is doing it mentally:
When we're given the setting of ax^2 + bx + c
We want to find two numbers that multiply to c and add to b. (If a isn't 1, then we need to add that into our calculation, but in this case a = 1)
So, what two numbers multiply to 18 and add to -11?
-9 and -2, so we rewrite the equation as (x-9)(x-2)
We then solve for x, x - 9 = 0, so x = 9 and x - 2 = 0, so x = 2
Second is we use the quadratic formula:
It would be