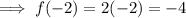Answer:
A and C
Explanation:
Piecewise functions have multiple pieces of curves/lines where each piece corresponds to its definition over an interval.
Given piecewise function:
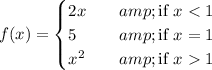
Therefore, the function has three definitions:
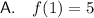
This statement is true as when x = 1, f(x) = 5.

This statement is false as when x is greater than 1, f(x) = x²:
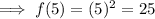
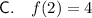
This statement is true as when x is greater than 1, f(x) = x²:
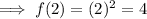
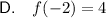
This statement is false as when x is less than 1, f(x) = 2x: