Answer:
|AC| = 132 cm (nearest centimetre)
Explanation:
Pythagoras Theorem
Pythagoras Theorem explains the relationship between the three sides of a right triangle. The formula is:
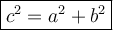
where:
- a and b are the legs of the right triangle
- c is the hypotenuse (longest side) of the right triangle.
From inspection of the given right triangle:
- a = AB = 45 cm
- b = BC = 124 cm
- c = AC
Substitute the given values into the formula and solve for AC:
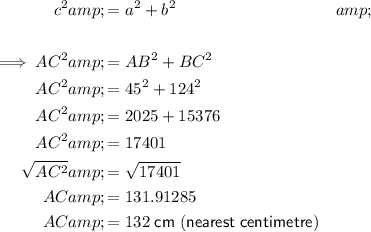
Therefore, |AC| is 132 cm to the nearest centimetre.