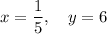Answer:
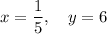
Explanation:
Given equations:
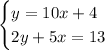
To solve the given equations by substitution, substitute the first equation into the second equation and solve for x:

Substitute the found value of x into the first equation and solve for y:
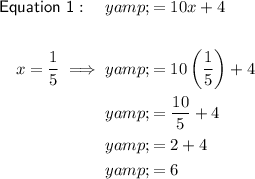
Therefore, the solution to the equations is: